Magnetic and electric fields exist nearly everywhere, and the following is a brief description of what these fields are, how they are created, and what effects they produce.
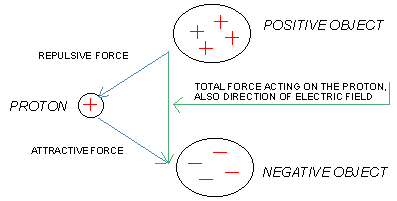
The concept of an "electric field" arose when electrons were observed to repel other electrons but attract protons. This attraction-repulsion was actually seen before the discovery of electrons or protons; early measurements studied the forces on objects that happened to acquire an excess or deficiency of electrons after being rubbed with cloth or fur. If two electrons are separated by one centimeter, each electron will experience a repulsive force of 2.3 x 10-24 gram-equivalents. Doubling the separation will reduce the force to one quarter. Doubling the number of electrons on one side will double the repulsive force acting on the lone electron on the other side. Most matter is neutral, so it contains an equal number of protons and electrons. However, sometimes electrons are deliberately or accidentally removed from one object, and deposited onto another object. If a proton (or other positive-charged body) is placed near these two charged objects, the proton will be attracted to the negative object, which has excess electrons, and simultaneously repelled from the positive one, which is missing some electrons. The total force acting on the proton is a measure of the electric field that the proton is exposed to. The direction of the force that acts on the proton is the same as the direction of the electric field and the strength of the force is proportional to the strength of the electric field. (The force that acts on the proton, in gram-equivalents, multiplied by 6 x 1016, gives the electric field in units of volts per meter or V/M.) If an electron were substituted for the proton, the force would be of the same strength but in the opposite direction of the electric field. If two protons "tied" together were substituted for the single proton, they would experience twice as much total force. (Fig.1)

If the terminals of a battery are connected to two large metal plates (Fig. 2), the + plate will lose some electrons, which will flow through the battery to the - plate.
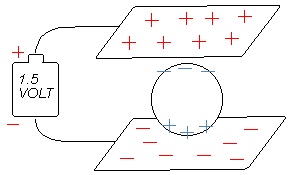
A battery therefore acts as an electron "pump", ultimately establishing an electric field between the plates (a proton would be attracted toward the - plate and repelled from the +). The strength of this electric field equals the battery voltage divided by the distance between the plates (usually measured in meters). For example, if the battery is 1.5 volts and the spacing is one meter, the electric field is 1.5 Volts per Meter (V/M), but if the spacing is reduced to 1/2 meter, the electric field increases to 3 V/m, which doubles the force that a single proton, if placed in the center, would experience. Any charged particle placed between the plates of Fig. 2 would experience a force downward if the particle were positive, or upward if negative. If a conductive body (such as a piece of metal or a cup of salt water) is placed between the plates as shown in Fig. 2, the charged particles inside the conductor will quickly shift position a little, to the final position shown. All conductive bodies contain charged particles that can freely move around. In metals these particles are the electrons from the outer part of the atom. In conductive liquids such as salt water, the conductive particles are called ions: positively-charged sodium atoms and negatively-charged chlorine atoms, which can move through the water. The charged particles shifted position simply because they were responding to the electric field from the battery and metal plates. A small fraction of a second after the conductive body was placed between the plates, the charged particles stopped moving, coming to rest in the final position shown. Ironically, this is the exact configuration of charges needed to produce zero electric field inside the conductive body. (Note that the conductive body is - on top and + on bottom, which means an upward-pointing electric field, whereas the plates try to produce a downward-pointing electric field. Within the conductive body, the upward and downward fields cancel each other.) Because no electric field now exists within the conductive body, the internal charged particles have stopped moving and the configuration is stable.
If the battery is subsequently reconnected to the plates in reverse, all charges in Fig. 2 will reorient so that - and + ultimately interchange after a small fraction of a second. The movement of charges is defined as an electric current, so that during that brief time the charges in the conductive body are reorienting themselves, a current is flowing. At all other times (when the charges are stable), no current flows in the conductive body. Therefore, inside a conductive body, no current flows and no internal electric field exists except during the periods when the outside electric field is changing.
Unlike the electric field, the magnetic field is not fundamental, That is, the concept of a magnetic force is not a separate force, but arises directly from the electric force, if the principles of Einstein's special relativity theory are applied to the electric force. Specifically, if two electrons are travelling parallel to each other, the electric force makes them repel each other, so the separation between them gradually increases. The speed at which this separation increases is not quite as high as would be predicted by electric repulsion alone. Something prevents the electrons from repelling each other as much as they might, and the faster the electrons are travelling, the less this repulsion.
In fact, if the electrons are travelling just less than the speed of light, they will hardly repel each other at all. An analysis of this system, with relativity effects included, shows that the ratio of the repulsive force between moving electrons to the repulsive force between stationary electrons is (l-Vl x V2/c2) : l. Here V1 and V2 are the speed of the two electrons and c is the speed of light. The V1 x V2/c2 term acts as an attractive force (because it reduces the repulsive force). This term represents the magnetic force between the electrons. The magnetic force can cause two parallel wires to attract if they are both carrying an electric current (that is, a flow of electrons). This is in spite of the fact that wires are usually electrically neutral, so that no direct electric repulsion (or attraction) usually occurs between the wires. Two parallel wires each 40" (100 cm) long that are one cm apart and carry one amp of current will attract each other with a force of 0.002 gram-equivalents due to the magnetic force. The force will double if the current in either wire is doubled or if the separation is reduced to 1/2 cm. If the direction of current in one of the wires is reversed, the force will become repulsive, but will remain the same strength.
The current in the first wire is said to create a magnetic field that acts on the current in the second wire. In a similar way, the second wire also acts on the first. The attraction is mutual; the first wire attracts the second with the same amount of force that the second attracts the first. The amount of magnetic force a wire experiences is proportional to the product of magnetic field strength that the wire is subjected to, times the length of the wire, times the amount of current (in amps) the wire is carrying . The direction of the force is somewhat unexpected compared to the direction of the magnetic field; it is at right angles both to the direction of the magnetic field and the direction of the current (Fig. 3).

Besides being influenced by a magnetic field, a wire that is carrying a current also produces a magnetic field (however, the wire does not experience any overall force due to its own self-generated field). If the wire is long, the field strength is double at half the distance from the wire and is four times as much at a quarter the distance. The direction of the field is shown in Fig. 4.
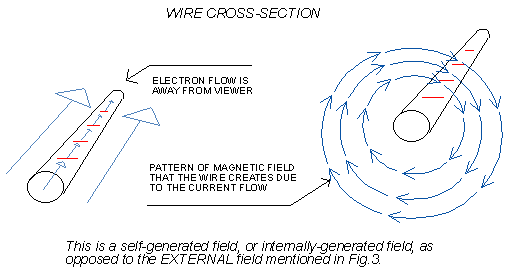
A wire that carries one amp will have a magnetic field of 0.00002 Tesla, or 200 milligauss (mG), a distance of one cm away. At two cm the field will be one half as much. Coils of wire that are carrying current, and also bar magnets, produce the classic magnetic field pattern shown in Fig. 5. (The bar is made of a material that needs "help" from electric current, to achieve and sustain magnetization.)
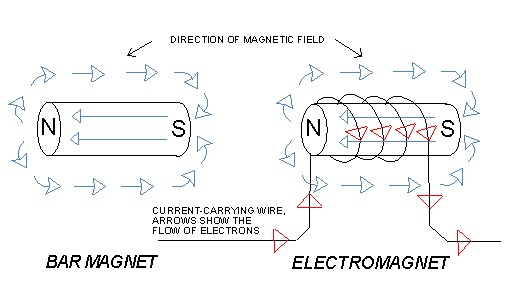
Technically Tesla and milligauss are called units of flux density, not magnetic field strength, but the difference is not important. The arrows (Fig. 5) are, in some popular illustrations, connected to form continuous "lines of force", but this is a misleading concept. The magnetic field is not concentrated along certain "lines" in the same way that, for example, atmospheric winds are sometimes concentrated along "jet streams". The magnetic field from a bar magnet smoothly decreases in strength as one moves away from the magnet and exists even very far from the magnet. Fig. 5 merely shows which direction the field happens to be pointing at several arbitrarily selected points near the magnet.
A coil-type electromagnet has a similar magnetic field pattern (Fig. 5). For both a bar magnet and an electromagnet, the magnetic field originates from current that circulates around the magnet. Certain types of metal; iron, steel, nickel, and vanadium; internally produce this circulating current without the help of a battery or wires (which are needed by an electromagnet). These metals are called ferromagnetic and their single outer electrons each produce a tiny, circulating current due to the electron orbits. All electrons in a ferromagnet (if fully magnetized) spin in the same direction. That is, if you look straight at the north pole of a magnet, all the outer electrons are spinning clockwise. (As you look at the south pole, all spin counterclockwise.) Having several small currents inside the bar magnet circulating clockwise is equivalent to having a significant clockwise current circulating on the outer surface of the bar magnet (which is equivalent to having a coil of wire carrying a significant amount of current around the bar as in Fig. 5). If two such magnets are brought close together with the "north" of one facing the "south" of the other, they will attract. This attraction is because the electron currents spin in the same direction around the edge of the magnets. (Remember that two wires carrying current in the same direction attract each other. If the wires are bent into two loops that are parallel and close to each other, they will still attract as long as the current in the loops both circulate in the same direction). If the "north" of a magnet is brought close to the " north" of another magnet, they will repel, because the electron currents are circulating in opposite directions.
Two other important effects exist in electromagnetism. First, a changing electric field can produce a magnetic field. This means that if the battery voltage is gradually increased in Fig.1, the plates will acquire an ever-increasing amount of charge. Ignoring the conductive body in Fig.1, no charge will actually flow through the air gap between the + and - plates. Yet a magnetic field will be created in that gap as if charge were flowing. (The orientation of that magnetic field is similar to the arrows shown in Fig. 4, if you take an overhead view of Fig. 1, looking down through the top plate). Here, the changing electric field itself is creating the magnetic field.
The second effect is that a changing magnetic field can create an electric field. This is the basis of power transformers and electric power generation. One coil of wire (or one electromagnet as in Fig. 5) is placed close to another. An increasing current flow is established in the first coil, which creates an increasing magnetic field. The increasing magnetic field causes electrons to circulate around the second coil in such a way as to oppose the increasing magnetic field that the first coil is trying to establish. That is the second coil will try to create a "north" pole pointing toward the first if the first is trying to create a north pole pointing toward the second. The movement of electrons in the second coil will briefly and partially shield the magnetic field that the first coil is trying to establish, but the second coil will ultimately (after a fraction of a second) fail at shielding. The only way the second coil could permanently shield the field is if its wire were a perfect conductor (superconductor) that is short-circuited (that is, the two wire ends in Fig. 5 were connected together), so that the electrons could continue to circulate around forever, if necessary. If the second coil is left open-circuit a voltage difference will appear between the two wires. During the period that the field of the first coil is increasing, the second coil can thus act as a battery, generating power. If the first coil is instead replaced by a vibrating or rotating bar magnet, the second coil will still generate power. This is the operational basis of electric turbines. The changing magnetic field creates an electric field directly in the wire (and in all other regions of space nearby) which causes electrons in the wire to move. The amount of voltage generated is proportional to the total length of wire in all the loops. A changing magnetic field will also create an electric field in the human body, which causes a current to flow. The current is at right angles to the direction of the changing magnetic field, and is strongest near the extremities of a person. Current tends to flow along the outer surface of the body. Its strength is proportional to the rate at which the field changes (or for an AC field, current is proportional to the magnetic field strength times the frequency of oscillation). For a 60 Hz (60 oscillations per second) field with a strength of three milligauss (root-mean-square measurement), a current is created in an adult which is on average one billionth amp per square centimeter of cross-sectional area. (The current per area is actually several times that near the head but is near zero at the geometric center of the body.) For these currents induced by magnetic fields, the current per area increases proportional to the linear size of the organism. For example, an animal only 1/10 the size of an adult person (that is, only 7" long) would average 1/10 as much current per area.
An AC electric field will also create a current in the body, as in the conductive body of Fig. 2. This current usually flows in the same direction as the electric field and is fairly uniform throughout the body. As with magnetic field current the current from an AC electric field is proportional to the frequency multiplied by the strength. For an adult, a 2000 V/m electric field at 60 Hz will create on average one billionth amp per square cm. Unlike the case of magnetic current the electric current per square centimeter does not scale down for a small animal.
The changing-electric-creates-magnetic and changing-magnetic-creates-electric effects make possible electromagnetic waves (radio waves). These waves are usually emitted from a wire (antenna) connected to an oscillator (in essence, a battery that repeatedly reverses polarity very fast). The antenna rapidly oscillates between + and - creating a rapidly-changing electric field. Most radio waves are in the frequency range from half a million to several billion oscillations per second. That rapidly-changing electric field (which is vertical) creates a rapidly-changing magnetic field (which is horizontal and "wrapped around" the antenna). The magnetic field in turn creates an electric field which reinforces the existing electric field. Because of this reinforcement the strength of the electric field far from the antenna is much greater than it would be without the reinforcement. For example if a one foot antenna is connected to one volt DC (that is, the electric field is not oscillating), the electric field one mile away will be 1/100 billion V/m. However, if that same one volt is continuously reversed 200 million times per second (the proper frequency for a one foot antenna to emit radio waves with maximum efficiency), the peak electric field one mile away will be 1/3000 V/m, or 33 million times higher. (A1so, the peak magnetic field there will be about 1/100,000 milligauss). Clearly, by using radiowaves, the electric (and magnetic) fields can be carried a long distance. The only "catch" is that the oscillation frequency must be fast; in the time required for one oscillation, light should travel a distance no more than 4 times the length of the antenna. If the oscillation frequency is much slower than this, very little true radio waves will be emitted by the antenna, and mostly only slow electric field (with no reinforcing magnetic field) will be emitted. This pure electric field will not carry very far. Similarly for a coil of wire with an AC current, a true radio wave is emitted only if the frequency of the current is fast enough compared to the dimension of the coil. Otherwise the field will be almost pure magnetic with very little reinforcing electric field. (A true radio wave has an exact fixed ratio of electric field strength to magnetic field strength. For every 30 V/m of electric field, there is 1 milligauss of magnetic.)
A one foot antenna, as previously mentioned, requires an oscillation frequency of about 200 million per second (200 MHz) for efficient radio transmission. A 10 foot antenna requires 20 MHz. For the AC frequencies typically encountered in the home (60, 180, and 300 oscillations per second are typical from power line current, and up to 17,000-35,000 from the horizontal scan of TV and computer monitors), antennas and coils would have to be at least several miles long to emit true radio waves. Because the devices that emit these fields (vacuum cleaners, fluorescent lights, etc.) are much smaller than that, household sources of fields are often pure magnetic (from wires or coils that carry AC current), pure electric (from metal plates or wires that are connected to the electric "hot" wire, regardless of whether any current is present), or some mix of magnetic and electric which is not necessarily in the ratio of 30 V/m per 1 milligauss that is standard for radio waves. In other words, if you measure just the electric field of a radio wave, you can easily calculate how strong the magnetic field of that wave must be, but if you measure just the AC electric field at some point near an appliance, there is no way to calculate what the magnetic field strength is. It must be measured. Also, unlike radio waves, household field sources tend to die off quickly in strength when you're more than a few feet (sometimes a few tens of feet) away.
Even though the concept of magnetic and electric fields is somewhat artificial and was only developed to quantify how moving and stationary charges attract and repel each other, the fields are real in one sense; they carry energy. Recall in Fig. 2 that the battery had to "pump" some charges to establish an electric field. This action required the expenditure of energy, and whenever an electric field is created, a certain amount of energy (in the form of repositioning of electric charges against the direction they "want" to go) is required. This energy can be recovered when the electric field is short-circuited. Indeed, the plates in Fig. 2 act as a mini-battery. Similarly, the establishment of a magnetic field (by accelerating electrons in a wire so they travel at a certain speed) requires energy, which can similarly be recovered. A 1 milligauss field contains 4 billionths (4 x 10-9) watt-second of energy per cubic meter of space. Surprisingly, an electric field of 30 V/m contains exactly the same amount of energy. (Remember the ratio of electric to magnetic fields for a radio wave? This is not just coincidence.) Ten times as much field (10 milligauss or 300 V/m) has 100 times the energy. Also, as might be expected, two cubic meters of space has twice as much energy as one cubic meter.
Because of the energy carried by electric and
magnetic fields, radio waves carry energy outward at the speed of light. If
at a certain distance from an antenna, the average electric field is 30 V/m,
then the average magnetic field will be 1 milligauss and the radio wave will
carry a power of 0.24 milliwatt through each square centimeter of cross section
the wave travels through. At twice the distance from the antenna, the electric
field is 15 V/m, the magnetic field is 0.5 milligauss, and the power is 0.06
milliwatt per square centimeter. (That is, when the electric and magnetic fields
go down to 1/2, the power per area goes down to 1/4.)